ตารางสูตรคำนวณน้ำหนักโลหะผสมอลูมิเนียม

1. การตรวจสอบหลักการทางกายภาพของสูตรแกนกลาง

กฎการอนุรักษ์มวล

สูตรทั้งหมดขึ้นอยู่กับลักษณะทางกายภาพของ m=ρ×V (มวล = ความหนาแน่น × ปริมาตร)

ค่าความหนาแน่น

ความหนาแน่นเชิงทฤษฎีของอะลูมิเนียมบริสุทธิ์: 2,698 กก./ม.³ (20℃)

ค่าประมาณ 2,700 กก./ม.³ ถือว่าเหมาะสมสำหรับการคำนวณทางอุตสาหกรรม (ข้อผิดพลาด < 0.1%)

2. การตรวจสอบความเข้มงวดของสูตรทางเรขาคณิต

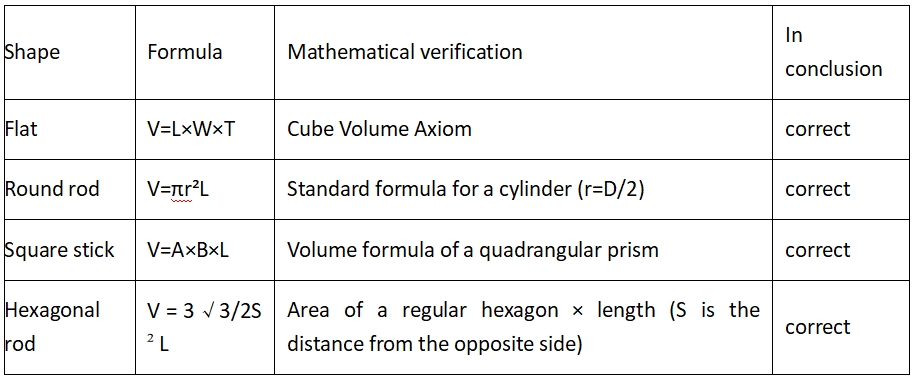
2.1. สูตรปริมาตรเรขาคณิตมาตรฐาน

2.2. การตรวจสอบสูตรท่ออย่างละเอียด

ข้อจำกัดของสูตรท่อสี่เหลี่ยม:

นี่เป็นจริงเมื่อความหนาของผนังท่อสม่ำเสมอและมุมด้านในเป็นมุมฉาก (ท่อสี่เหลี่ยมจริงมีการเปลี่ยนแปลงแบบโค้งมน และข้อผิดพลาดทางทฤษฎีอยู่ที่ประมาณ 1-3%)

3. การตรวจสอบความสอดคล้องของระบบหน่วย

การตรวจสอบจุดเสี่ยงในการคำนวณข้ามหน่วย

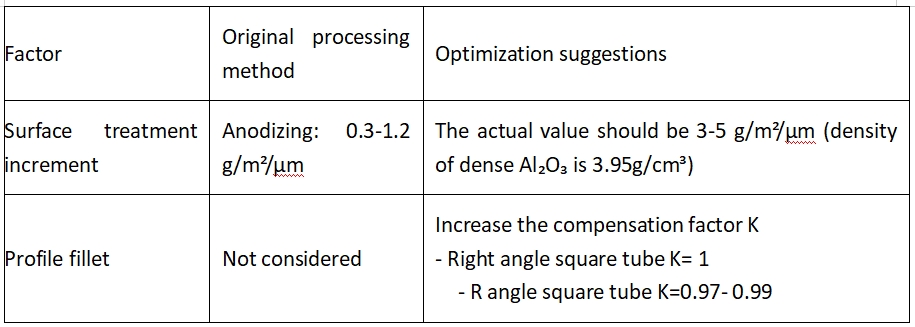
4. การแก้ไขความเหมาะสมทางวิศวกรรม

4.1. การชดเชยปัจจัยที่ไม่เหมาะ

4.2. การวัดปริมาณผลกระทบจากความคลาดเคลื่อน

ความคลาดเคลื่อนของความหนา ±10% → ความคลาดเคลื่อนของน้ำหนัก ±(8% ~ 12%) (ชิ้นส่วนที่มีผนังบางมีความอ่อนไหวมากกว่า)

เฉลย: W จริง = W ตามทฤษฎี × (1 + Δt / t) ( Δt : ค่าเบี่ยงเบนความหนา)

5. การทดสอบเงื่อนไขขอบเขต

การตรวจสอบกรณีสุดขั้ว:

สถานการณ์ความผิดปกติของความหนาแน่น

โลหะผสม 7xxx (7075): ความหนาแน่นที่วัดได้ 2.810 g/cm³ → หากใช้ 2.7g/cm³ โดยไม่ได้ตั้งใจ ข้อผิดพลาดคือ +4.1%

ตารางสูตร

4t(A + B)- 4t² เป็นการคำนวณทางวิศวกรรมมาตรฐานที่คำนวณได้โดยการคูณเส้นรอบวงของส่วนตัดด้วยความหนาของผนัง จากนั้นลบมุมทั้งสี่ออก

ตัวอย่างการคำนวณ:

แผ่นอลูมิเนียม 1.6061(1000 × 500 × 10 มม., ยาว 2 ม.): W = 1000 × 500 × 2 × 0.0027 = 27 กก.

ท่อกลม 2.7075(เส้นผ่านศูนย์กลางภายนอก 50 มม. ความหนาของผนัง 3 มม. ความยาว 1.5 ม.): W = [(50-3)×3×3.1416×1.5]×0.00283 ≈ 5.65 กก.

3. ท่อสี่เหลี่ยม(40×40×2มม. ยาว 3ม.): W = [2×2×(40+40-4)×3]×0.0027×0.98 ≈ 2.42 กก.

เวิร์กโฟลว์ที่แนะนำ

1. เลือกความหนาแน่น → 2. วัดขนาดจริง → 3. เลือกปัจจัยชดเชย → 4. คำนวณโดยใช้สูตร